CSC 220 Lab 8/Homework 6 - Arithmetic Expression Trees

Tuesday, October 19, 2004

Due: Monday, November 1, 2004

Will not be accepted later than Friday, November 5, 2004. This assignment will count as one lab grade and one homework grade. Do not leave this assignment to the last minute.

Sections of this document:
[Summary] [Exercises] [Valid Input and Error Messages] [Parsing Strategies] [Resources] [Hand in]

Summary

In this assignment, you will extend the basic binary tree implementation of Homework 5 to handle arithmetic expression trees. You will implement some methods for building and traversing the expression trees, and will learn to think carefully about handling input errors. This assignment will require a little more thought and design than previous assignments, but if you get stuck, don't hesitate to contact me -- in office hours, by email, etc. But start working early on this problem -- don't leave it till the last minute.

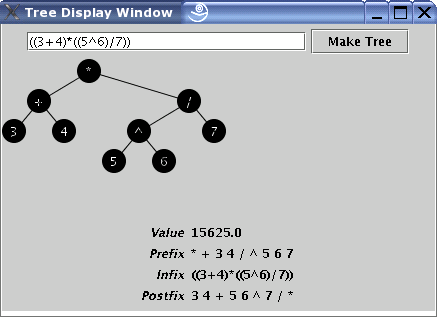
The code you write will be able to parse and evaluate fully parenthesized arithmetic expressions, such as "((3+4)*((5^6)/7))".

I will provide you with a ViewTree class to test your implementation. The command java ViewTree "((3+4)*((5^6)/7))" will bring up the following window. The drawing is produced by the ViewTree code (using a technique described in the textbook), but the values in the four lines at the bottom will be produced by calling your code for the TreeExpression class (described below).

Exercises

You should already have written a class that implements the BinaryTree interface. Now you should write a class called TreeExpression that implements the Expression interface. 
/* Represents an arithmetic expression */                        

public interface Expression {

    /* Converts to a string in prefix notation 
     * (i.e. a preorder traversal of the tree)    */
    public String prefix();

    /* Converts to a string in infix notation 
     * (i.e. an inorder traversal of the tree)    */
    public String infix();

    /* Converts to a string in postfix notation
     * (i.e. a postorder traversal of the tree)   */
    public String postfix();

    /* Finds the value of the expression          */
    public double value();

}

Your TreeExpression class should implement not only Expression but also BinaryTree, which you can achieve by having TreeExpression extend your binary tree class. By implementing both interfaces, you will allow the ViewTree class to call methods of BinaryTree on the expression in order to display the expression's tree.

Remember that TreeExpression extends your binary tree class. That means that every TreeExpression actually is a binary tree (augmented with some extra methods in order to implement Expression). It doesn't have to contain another binary tree.

Your TreeExpression class should have a constructor that takes a string argument such as "((3+4)*((5^6)/7))" and builds up an expression tree from it. ViewTree will call this constructor. If the string is invalid, the constructor should throw an InvalidExpressionException that contains an appropriately detailed error message as described further below. This is the only exception that ViewTree knows how to handle, so you should be careful not to throw any others. 
/** Thrown in response to a string that is not a legal                
 * arithmetic expression.  The String argument may be shown
 * to the user, so it should clearly explain what and where 
 * the trouble is.
 */

public class InvalidExpressionException extends Exception {  
  public InvalidExpressionException(String err) {
    super(err);  // just call the general Exception constructor
  }
}

You will probably want to test your constructor right away using the ViewTree class. So write temporary stubs for the other methods. (I.e. just return bogus values like "unknown" and 0.0.) Then you should at least be able to see the tree drawn graphically.

Once your constructor is working properly, you can fill in the other methods of the TreeExpression class. There is some discussion in the textbook about how to do this.

Of course, you do not have to just use the ViewTree class for testing. If you can't get it to work quite well at first, or if you want a more thorough test, then write your own test code.

Valid Input and Error Messages

The expressions that your program should handle will be fully parenthesized infix expressions. Thus, 5+2*4 will not be a legal input; it must be written as (5+(2*4)). This saves you from having to deal with operator precedence rules ("order of operations").

The numbers in the arithmetic expressions should be integers only, not real numbers. (Although, when you evaluate the value of an expression tree, you should perform real number evaluation, especially for the division operation.) Any integer by itself will be a legal input. Then, if s1 and s2 are legal expression strings, so are the following five parenthesized combinations: (s1+s2), (s1-s2), (s1*s2), (s1/s2), (s1^s2). Whitespace may appear anywhere in the string between parentheses, operators and numbers.

Some examples of valid expressions:

When your code encounters an invalid expression, it should throw an InvalidExpressionException whose string argument is a clear error message. This error message should tell the user what problem was encountered and where it was encountered. Your error messages should be comparable in their level of detail to the following examples, although yours might be different depending on how your solution detects that an error occurred:

Possible Strategies for Parsing Expressions

The nodes of your binary tree store Objects as their elements, but what kind of objects? You should probably store an Integer at each external node, and a Character such as + at each input node.

How do you convert a fully parenthesized expression string into a tree? If the string is of legal form, one of two cases must hold: (a) The string is just a number, in which case you can just form a one-node tree, or (b) The string starts with a left parenthesis, in which case it must have the form (s1 c s2) where c is an operator character. There are at least three possible strategies:

  1. In case (b) above, you can scan the string to find the operator character, going left to right and counting +1 for left parentheses and -1 for right parentheses. Then use the substring() method to extract the two subexpressions that are arguments to that operator. Recursively build the left and right child subtrees out of these substrings and then put them together in a new tree with the operator at the root.

    This is not as inefficient as it may seem, since creating a substring takes O(1) time. It doesn't require any copying of characters; internally, a substring is represented as a pointer to the original string together with a pair of integers that indicate the extent of the substring.

    But it is nonetheless a somewhat time-inefficient strategy: each character will be repeatedly scanned (though not copied), once for every expression it's part of.

    If you use this strategy, be especially careful to handle whitespace. Also note that your error messages are likely to look a bit different from the examples given earlier.

    This strategy also has to be careful about minus and plus symbols. The - symbol in -3 is not a subtraction operator, and the second + symbol in (5 + +3) is not an addition operator. Probably the easiest solution is to look at the character before the minus or plus symbol (ignoring whitespace); that should let you figure out what kind of minus or plus it is.

     

  2. You can write a method that removes the smallest complete expression from the front of the string and returns a tree for it. This can also be implemented recursively. If the string is just a number, you return a 1-node tree. If it has the form (s1 c s2), then you do 5 steps: remove a left parenthesis, recursively remove a subexpression s1, remove an operator character c, recursively remove a subexpression s2 and finally remove the right parenthesis. You can then combine the operator with the two subexpression trees to get a tree to return.

    If any of these steps go wrong, it signals that something is wrong with the input string, so you should throw an exception with a detailed error message. For example, you might be ready to remove an operator character, but there isn't one at the front of the string for you.

     

  3. The previous two techniques use recursion. Recursion is a very nice way of keeping track of where you are and how to assemble the results. After all, when a method call returns, its caller remembers where to put the result in the tree and how to continue with its own computation.

    But you can also solve the problem without recursion. The idea is to process the string from left to right, building the tree as you go. Your "current node" in the tree keeps track of where you are in the computation. If you remove a number, it goes at the current node. If you remove a left parenthesis, you make the current external node internal (by giving it children with createExternal()), and descend to the new left child, which becomes the current node. If you remove an operator, then ... well, you get the idea.

    Again, if any of these steps go wrong, it signals a problem and you should throw an exception with a detailed error message. For example, the input string might inappropriately "tell" you to add children to a node that is already internal, or add an element to a node that already has one, or ... what else?

Regardless of whichever strategy you choose, your error messages should be designed to be useful to the user. Don't just report something like Can't add children to an internal node. Tell the user what is wrong with the string so that he or she knows how to fix it!

Resources

These files are also available in the class folder for lab8 from the networked M:\ drive on the computer lab machines.

Hand in

Hand in a printout of all the commented Java program files that are necessary to make your program run correctly, and also submit them online through VikingWeb. If you want, you can bundle all the files up into a zip archive so that you only have to upload one file to VikingWeb.

 

Acknowledgments: This assignment was prepared based on one developed by Prof. Jason Eisner (Johns Hopkins Univ.) The ViewTree code is reused from his development.

 

Last modified: Tue Oct 19 10:39:05 EDT 2004