Skip to main content.

Thursday, March 9, 2006
Due: Friday, March 24, 2006

Recursion

Recursion is a powerful programming technique that solves problems by breaking bigger or more complex problems into simpler ones. As the textbook says,

The term "recursion" refers to the fact that the same computation recurs, or occurs repeatedly, as the problem is solved. Recursion is often the most natural way of thinking about a problem, and there are some computations that are very difficult to perform without recursion.
In this lab, we will investigate a few simple examples of recursion to understand how to think "recursively."

Factorial

The factorial of a positive integer is the product of all non-negative integers less than or equal to that number. The symbol for factorial is "!" -- the exclamation mark. The formula for factorials, where n > 0, is:

n! = n * (n-1)!

Zero factorial is a special case, so 0! = 1.

For example, 5! is 120: 

1! = 1 * 0! = 1
2! = 2 * 1! = 2
3! = 3 * 2! = 6
4! = 4 * 3! = 24
5! = 5 * 4! = 120

In your Eclipse workspace, create a new project for this lab, and create a new class called "RecursiveLab". Write a method with the header: public static long factorial(int n). Let's think about how to fill in the body of this method. First, we need to consider the case when n=0. In that case, the method should just return 1. Write an if statement in the factorial method that checks for this case and returns 1.

Now think about what the method should return if n is greater than 1. It can compute the factorial of n by multiplying n times factorial(n-1). When a method like factorial makes a call to itself -- that is called recursion. Almost all of the time, the parameters of the recursive call should get "smaller" in some sense.

Write a main method that calls the factorial method to test it and prints out the result.

Iterative Factorial

You can also compute the factorial values iteratively, without using recursion. Write a non-recursive factorial method called iter_factorial(int n). Add code to your main method to test this method.

Greatest Common Divisor

A formula for finding the greatest common divisor (GCD) of two numbers was formulated by the mathematician Euclid around 300 BCE. The GCD of two numbers is the largest number that will divide into both numbers without any remainder. For example, the GCD of 12 and 16 is 4, the GCD of 18 and 12 is 6.

The basic algorithm is as follows:

Recall that in Java, the % operator computes the remainder. For example, to compute the GCD of 12 and 16, you compute 16 % 12 = 4

Now you need to compute the GCD of 12 and 4. 12 % 4 = 0

Therefore, the GCD is 4.

Write a recursive method that finds the GCD of two numbers using Euclid's algorithm. (You may assume that both inputs are positive.)

Write a tester program for your GCD class.

Components of a Recursive Method

As you should be able to notice from the exercises above, a recursive method solves a problem by using the solution of the same problem for simpler, or smaller, values. For the recursion to terminate, you need to make sure that the special case(s) of the smallest value(s) is handled by the method.

The call a method makes to itself is called a recursive call. The special case that a recursive method checks for to end the recursion is often called the "base case."

Recursive Helper Methods

Sometimes it is easier to find a recursive solution if you make a slight change to the problem you are trying to solve. You can write a recursive helper method to solve the modified instance of the problem, and then call the helper method to help solve the original problem.

6.

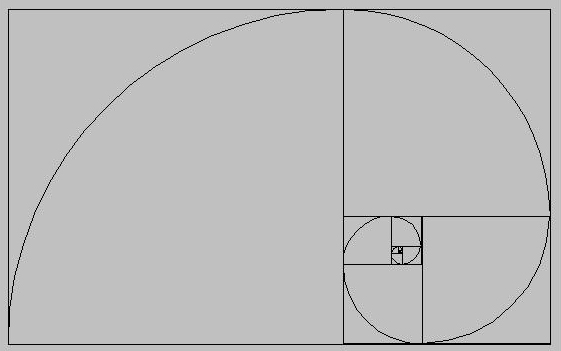
In the steps below, taken from the book's lab manual, you will write a program to draw the logarithmic spiral recursively.

The logarithmic spiral or Fibonacci spiral is a shape often found in nature. The nautilus shell is the classic example of the logarithmic spiral. Seed patterns in sunflowers and pinecones also demonstrate the spiral.



To construct a logarithmic spiral, begin with a "golden" rectangle. A golden rectangle is a rectangle with sides of length A and (Phi)*A, where (Phi) is the golden mean or the value ( 1 + sqrt(5) ) / 2 or 1.61803 . . . A square with length equal to the smallest side of the rectangle is drawn inside the rectangle. A quarter arc (arcAngle = 90 degrees) is drawn within this square. The remaining rectangle is also a golden rectangle. This remaining rectangle is divided into a square and another smaller golden rectangle. A quarter arc connected to the previous arc is drawn inside the square, and the remaining rectangle is once again subdivided with an arc drawn in it.

Create a panel in which to draw the spiral:

public class LogSpiralPanel extends JPanel 

Given the dimensions of the panel, draw the largest golden rectangle that will fit within the panel. Part of the code of the class has been provided for you:

import java.awt.Graphics2D;
import java.awt.Graphics;
import java.awt.Rectangle;
import java.awt.geom.Arc2D;
import javax.swing.JPanel;

public class LogSpiralPanel extends JPanel
{
   public void paintComponent(Graphics g)
   {
       Graphics2D g2 = (Graphics2D) g;
       /*
         Your code goes here.
         1. create the goldenRectangle (you can use getHeight() to obtain the side size
         2. draw the golden rectangle
         3. call the recursive helper method "recursiveDraw" which will draw the spiral
       */
   }

   /**
      Method that recursively draws a logarithmic spiral.
      @param x The upper left corner x-coordinate of the golden rectangle
      @param y The upper left corner y-coordinate of the golden rectangle
      @param side the smallest side size of the golden rectangle
      @param angle the angle (0, 90, 180 or 270) where the top of the golden rectangle is located.
      For the outermost golden rectangle, the angle is 90.
*/
    private void recursiveDraw(Graphics2D g2, double x, double y, double side, int angle)
    {
       // we'll do this in the next section. . .
    }

    

    private static final double GOLDEN_MEAN = (1 + Math.sqrt(5)) / 2;
}

What is the code of your completed paintComponent method?



7.

Now you will complete the code of the recursive helper method recursiveDraw. To recursively draw the logarithmic spiral, you first need to draw the square. The square's upper-left corner is at position (x, y), and its side size is side. Then you need to draw the arc. You can use the method drawArc that has been provided for you. Then you need to recursively call recursiveDraw to continue drawing the spiral recursively. Before making the recursive call you need to calculate the new side size, the new x-coordinate, the new y-coordinate and the new angle. Two methods calculateNewX and calculateNewY have been provided for you. You can use these methods to calculate the new x and y coordinate, but you need to calculate the new side size and the new angle yourself. Remember that the new side size is the difference between the sizes of the two sides of the current rectangle. The new angle is given by rotating the current angle 90 degrees in clock-wise direction.


public class LogSpiralPanel extends JPanel
{
    public void paintComponent(Graphics g)
    {
    . . .
    }

    /**
        Method that recursively draws a logarithmic spiral.
        @param x The upper left corner x-coordinate of the golden rectangle
        @param y The upper left corder y-coordinate of the golden rectangle
        @param side the smallest side size of the golden rectangle
        @param angle The angle (0, 90, 180 or 270) where the top of the         current golden rectangle is located.
        For the outermost golden rectangle, the angle is 90.
     */
    private void recursiveDraw(Graphics2D g2, double x, double y, double side, int angle)
    {
        /* Recursion ending condition: when the side is very small */
        . . .

        /* Draw the current square and arc */
        . . .

        /* Continue drawing the spiral recursively: calculate the new side size, calculate the new
            (x, y) coordinates and the new angle. Then, call "recursiveDraw" again. */
        . . .
    }

    /**
        Draws the arc of the current iteration.
        @param x The upper-left corner x-coordinate of the square
        @param y The upper-left corner y-coordinate of the square
        @param side The size of the side of the square (or the arc's radius)
        @param angle The angle (0, 90, 180 or 270) where the top of the current golden rectangle is located.
        For the outermost golden rectangle, the angle is 90.
    */
    private void drawArc(Graphics2D g2, double x, double y, double side, int angle)
    {
        double auxX = x;
        double auxY = y;
        if (angle == 0 || angle == 270)
            auxX = x - side;
        if (angle == 270 || angle == 180)
            auxY = y - side;
        Rectangle2D.Double boundingRectangle =
new Rectangle2D.Double(auxX, auxY, side * 2, side * 2);
        Arc2D.Double arc = new Arc2D.Double(boundingRectangle, angle, 90, Arc2D.OPEN);
        g2.draw(arc);
    }

    private double calculateNewX(double x, double angle, double side, double newSide)
    {
        if (angle == 0)
            x = x + side - newSide;
        else if (angle == 90)
            x = x + side;
        else if (angle == 270)
            x = x - newSide;
        return x;
    }

    private double calculateNewY(double y, double angle, double side, double newSide)
    {
        if (angle == 0)
            y = y + side;
        else if (angle == 180)
            y = y - newSide;
        else if (angle == 270)
            y = y + side - newSide;
        return y;
    }

    private static final double GOLDEN_MEAN = (1 + Math.sqrt(5)) / 2;
}

What is the code of your recursiveDraw method?


8.

Create a LogSpiralFrame class that will contain the LogSpiralPanel. Write a main method to construct and display the frame.

Homework Exercises

Over Spring break, your first assignment is to read Chapter 17 thoroughly. Make sure you do this. There may be a small in-class quiz on the chapter when we come back.

[60 points] Exercise P17.4 on page 659.

[40 points - extra credit] Exercise P17.5 on page 659.